详细了解哈夫曼树和背包问题

Posted on Edited on

详细了解哈夫曼树和背包问题

写在前面：

  • 最近在疯狂复习数据结构和算法，虽然看完了一部完整的视频。但是转眼看看自己手中的《剑指Offer》里面还是不是很清楚。。。而且最近也突然觉得自己知识和别人比起来就是一个渣渣。各种被人家吊打。。。
  • 这两个算法一个（哈夫曼树）是看最近视频动手实践的，一个(背包问题)是前段时间一个面试里面的题目，当时不知道这是一个系类的问题，昨天和大神聊完天之后才明白。所以乘着短暂的热情还在就记录下来先从哈夫曼树开始！！

1.哈夫曼树（实现基本的编码解码）

  • 简单定义：
    给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

    复杂的文字定义我觉得以后肯定不会看。。所以直接来一张哈夫曼树的构造过程简单明了。。

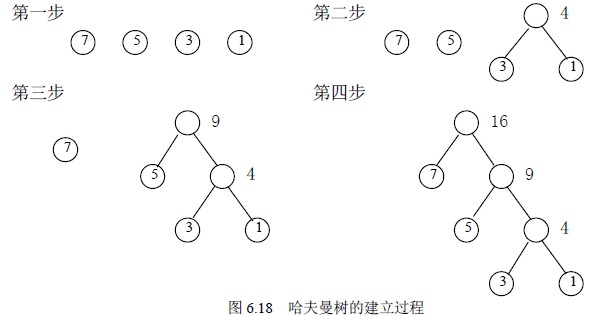
1.模型构造

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 节点类
	public static class Node implements Comparable<Node> {
		String data;
		double weight;
		Node leftChild;
		Node rightChild;
		Node parent;

		public boolean isLeftChild() {
			return parent != null && this == parent.leftChild;
		}

		public Node() {

		}

		public Node(String data, double weight) {
			this.data = data;
			this.weight = weight;
		}

		@Override
		public String toString() {
			return "Node [data=" + data + ", weight=" + weight + "]";
		}
		//队列排序依据
		public int compareTo(Node o) {
			return (int) (weight - o.weight);
		}

		public boolean isLeaf() {
			return data.length() == 1;
		}
	}

包含属性:

属性 定义 类型
data 数据 String
weight 权值 double
leftChild 左节点 Node
rightChild 右节点 Node
parent 父节点 Node

2.统计字符出现的次数，用出现的次数作为权值

  • 这里实现的思路是：将出现的字符串(C)和次数(count)保存为一个Map<字符，次数>对象,然后再保存为List集合
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
   public static Map<Character, Integer> statistics(char[] charArray) {
	Map<Character, Integer> map = new HashMap<Character, Integer>();
	for (char c : charArray) {
		Character character = new Character(c);
		if (map.containsKey(character)) {
			map.put(character, map.get(character) + 1);
		} else {
			map.put(character, 1);
		}
	}
	return map;
}
public static List<Node> statisticsProbability(Map<Character, Integer> maps) {
	List<Node> list = new ArrayList<TestHuffmanTree_Encode_Decode.Node>();
	for (Map.Entry<Character, Integer> map : maps.entrySet()) {
		Node node = new Node(map.getKey().toString(), map.getValue());
		list.add(node);
	}
	return list;
}

3.根据统计的List进行哈夫曼树的构造

首先List中保存的就是Node集合，其中Node的data就是字符串，Node的weight就是出现的次数也就是权值
哈夫曼树的构造:

  • 首先利用Java中的priorityQueue方法进行模拟队列
    priorityQueue的用法 其中主要的方法：
    方法 作用
    add 将指定元素插入到次优先级队列
    poll 获取并且移除队列头
    peek 获取但是不移出队列
  • 将List中的数据保存到队列里面去
1
2
3
4
  PriorityQueue<Node> priorityQueue = new PriorityQueue<Node>();
for (int i = 0; i < nodes.size(); i++) {
	priorityQueue.add(nodes.get(i));
}
  • 然后利用poll方法获取队列头节点,这里可能就由疑问了，哈夫曼树不是要求按照权值最小的两个开始组成树嘛。这里为什么随便从队列里面弄两个出来就可以。
    其实是这样的;在Node定义的时候实现了Comparable接口并且实现了compareTo（E e）方法，这里其实就已经实现了队列里面的排序
  • 然后构建两个子节点的父节点，并且声明三者之间的关系(父子，左右)
1
2
3
4
5
6
7
8
9
         // 构建父节点
Node sumNode = new Node(node1.data + node2.data, node1.weight
		+ node2.weight);

sumNode.leftChild = node1;
sumNode.rightChild = node2;

node1.parent = sumNode;
node2.parent = sumNode;
  • 然后再将父节点保存到队列中去:这样做的目的是为了得到根节点
    1
    priorityQueue.add(sumNode);
  • 最后返回根节点 priorityQueue.poll();

这样，到这里哈夫曼树的构建就完成了，但是既然学习了就深入一点，
哈夫曼树的最长用途就是用来文件压缩，因为我们知道发送一句话的时候并不是每个字母出现的频率都是一样的，有的出现的多有的出现的少，但是如果还是使用一样额编码那样会有很大的消耗，所以这里我们就用哈夫曼树实现对字符串的编码和解码