最近翻到之前的 如何开发一个自己的 RPC 框架的文章,突然对里面提及的“一致性 Hash 算法”很感兴趣,之前面试的时候有了解过,但是时间长易忘记,所以趁今天有时间,详细地了解一下这个算法。
为什么需要一致性 Hash
在分布式系统中,存在这么一个场景:
- 需要将 10w + 的数据,分别缓存到 3 台服务器上
这个时候,很自然地就想到了使用数据的唯一编号 id 和 服务器的数量 3 进行取模id%3,得到的结果代表缓存的目标服务器。
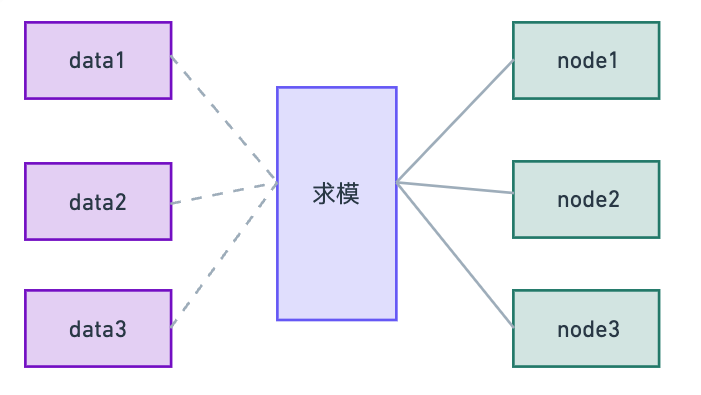
但是上面的方案在生产环境中是不可用的,因为生产环境会涉及到频繁地增加或者减少机器。如果增加一台机器,那么所有缓存数据的目标服务器都需要重新计算,会导致整个服务出现大面积不可用的情况。
在上面这个背景下,就诞生了一致性 Hash这个算法。
一致性 Hash 的原理
想象一下:
基于上面的想法,我们可以将所有的节点根据 ip 对一个固定值 2^32 进行求模,得到一个 0~2^32-1 之间的值
然后放在一个 0~2^32-1 的环上
Hash 环
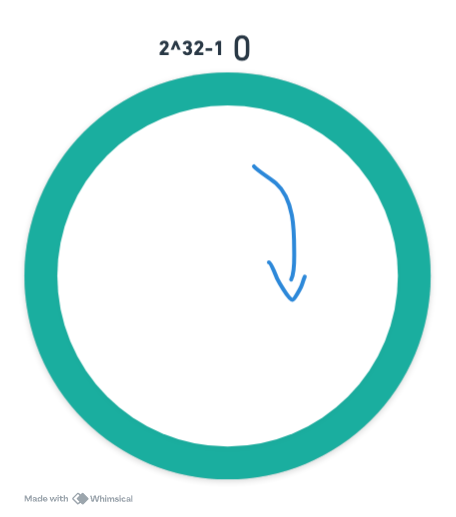
根据服务器的 ip,对 2^32 进行取模,然后分布到 hash 环上
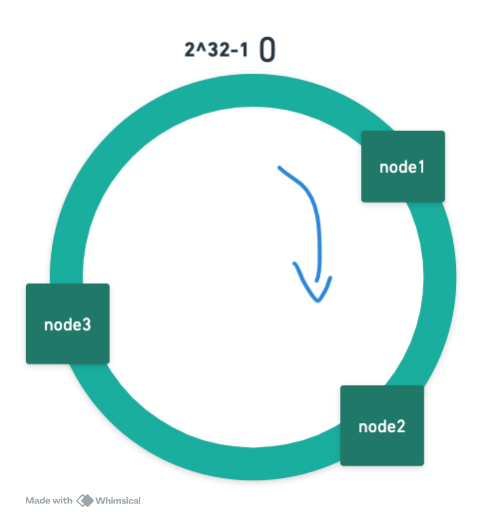
将缓存数据存放到服务器上:
和服务器一样,将数据的唯一编号对 2^32 进行取模,得到的值进行顺时针查找,找到最近的服务器进行存放
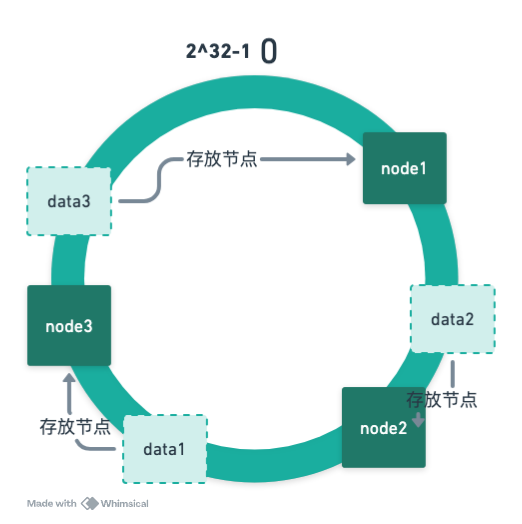
服务器缩容
当删掉 node1 机器后,data3 将自动找到 node2服务器,只会影响单台服务器
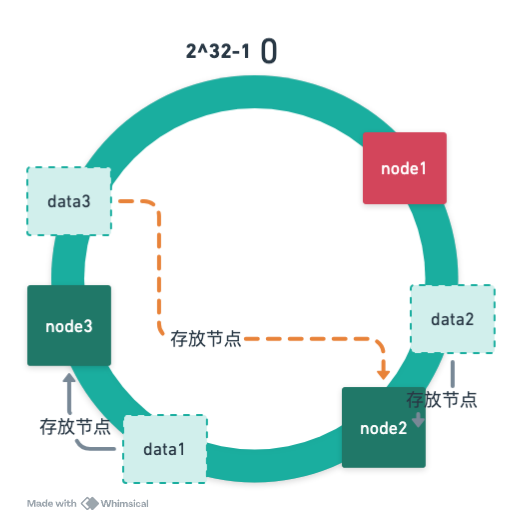
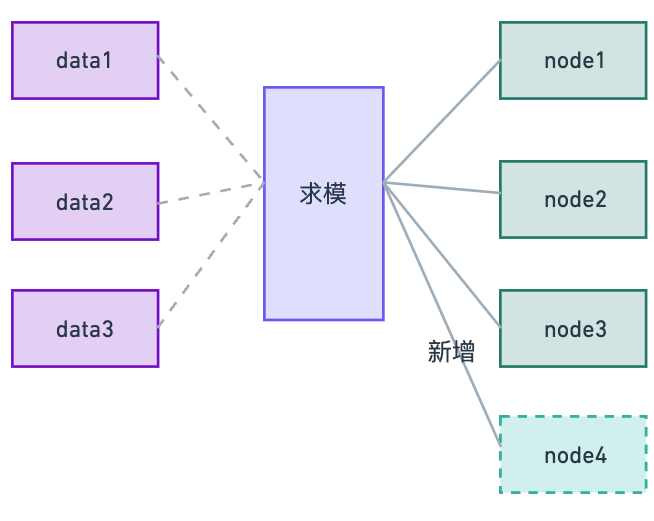
服务器扩容
当增加 node4 节点后,也只会影响 data3 的数据,不会导致其他数据全部重新缓存
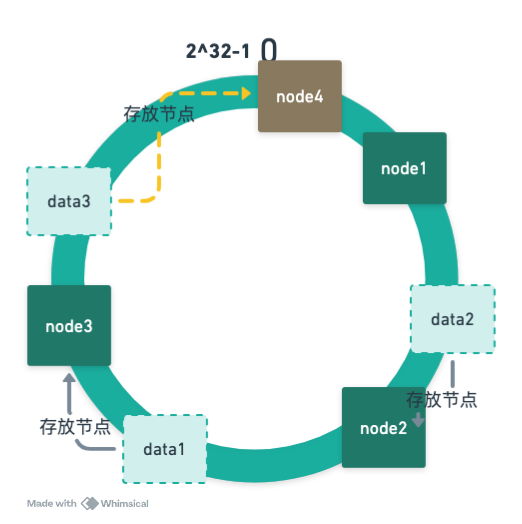
数据倾斜
什么是数据倾斜呢?

可以看到数据全部都根据顺时针的查找找到了node1,导致 node1 承担了大部分的缓存任务。为了解决这个问题,引入了虚拟节点的概念
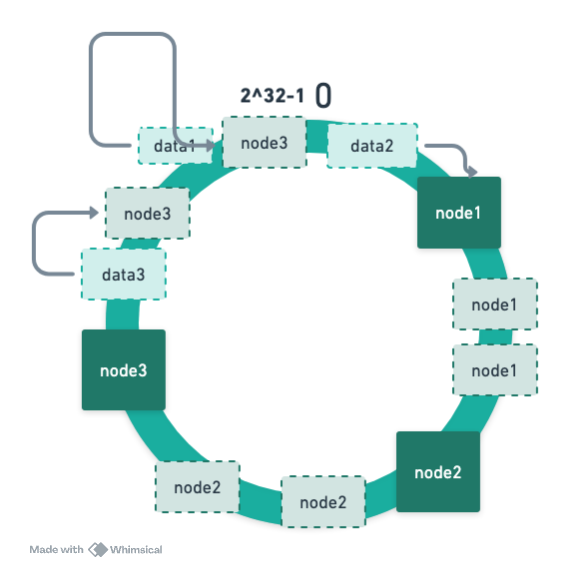
从代码出发,如何实现一致性 Hash
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
|
public static class ConsistentHash<T> {
private final NavigableMap<Long, T> ring = new TreeMap<>();
private final int virtualNodes;
private final HashFunction hash;
private final Map<T, List<Long>> nodeToReplicas = new HashMap<>();
public ConsistentHash(int virtualNodes) {
this(virtualNodes, new MD5Hash());
}
public ConsistentHash(int virtualNodes, HashFunction hash) {
if (virtualNodes <= 0) throw new IllegalArgumentException("virtualNodes must > 0");
this.virtualNodes = virtualNodes;
this.hash = hash;
}
public synchronized void addNode(T node) {
if (nodeToReplicas.containsKey(node)) return;
List<Long> replicas = new ArrayList<>(virtualNodes);
for (int i = 0; i < virtualNodes; i++) {
long h = hash.hash(nodeId(node, i));
ring.put(h, node);
replicas.add(h);
}
nodeToReplicas.put(node, replicas);
}
public synchronized void removeNode(T node) {
List<Long> replicas = nodeToReplicas.remove(node);
if (replicas == null) return;
for (Long h : replicas) {
ring.remove(h);
}
}
public synchronized T getNode(Object key) {
if (ring.isEmpty()) return null;
long h = hash.hash(String.valueOf(key));
Map.Entry<Long, T> entry = ring.ceilingEntry(h);
if (entry == null) {
return ring.firstEntry().getValue();
}
return entry.getValue();
}
public synchronized Set<T> nodes() {
return Collections.unmodifiableSet(nodeToReplicas.keySet());
}
public synchronized int ringSize() {
return ring.size();
}
private String nodeId(T node, int replicaIndex) {
return node.toString() + "##VN" + replicaIndex;
}
}
public interface HashFunction {
long hash(String key);
}
public static class MD5Hash implements HashFunction {
private final MessageDigest md;
public MD5Hash() {
try {
this.md = MessageDigest.getInstance("MD5");
} catch (Exception e) {
throw new RuntimeException(e);
}
}
@Override
public long hash(String key) {
byte[] digest;
synchronized (md) {
md.reset();
md.update(key.getBytes(StandardCharsets.UTF_8));
digest = md.digest();
}
int val = ByteBuffer.wrap(digest).getInt();
return val & 0xFFFFFFFFL;
}
}
|
其中使用到了 NavigableMap
- 基本概念
- NavigableMap<K,V> 是 SortedMap<K,V> 的子接口,支持对键 按自然顺序 或者 自定义比较器顺序 排序。
- 在 SortedMap 的基础上,NavigableMap 提供了更丰富的 导航(navigation)方法,可以根据某个 key 快速获取比它大/小的元素。
常见实现类:
- TreeMap(最常用,基于红黑树实现,支持有序和高效导航)。
主要方法
- 查找
1
2
3
4
5
6
7
8
9
10
11
| Map.Entry<K,V> lowerEntry(K key);
K lowerKey(K key);
Map.Entry<K,V> floorEntry(K key);
K floorKey(K key);
Map.Entry<K,V> ceilingEntry(K key);
K ceilingKey(K key);
Map.Entry<K,V> higherEntry(K key);
K higherKey(K key);
|
- 获取首位元素
1
2
3
4
5
| Map.Entry<K,V> firstEntry();
Map.Entry<K,V> lastEntry();
Map.Entry<K,V> pollFirstEntry();
Map.Entry<K,V> pollLastEntry();
|







